APPENDIX E: 3D Stars
3D STAR EQUATIONS
January 15, 2013
Once you have a 3D star constructed you no longer have to do the multiplication or division for an equation. It simply becomes an add and subtract problem. Neither do you have to keep adding infinite rays to your star.
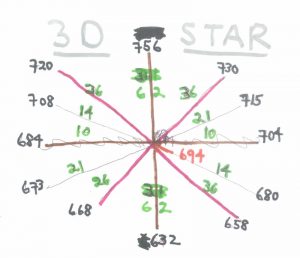
Pick the first number of 3 numbers. Say 673. Add a higher number, 720, which is 26 (green) more. Subtract 21 (green) from 720 to get 699 as the middle number (green = 47 or 5) between 673 and 720. The middle number is 26 more than 673 and 21 less than 720.
What I just performed mathematically is the same as:
673 (21) + 720 (26) = 699 (47)
Let’s do another example. You can figure out the green number for 708 by subtracting 694 from it.
708 – 694 = 14 (green)
Now let’s add 668. The green number is 26.
Add 14 to 668. 682.
Simple! You have just added:
708 (14) + 668 (26) = 682 (40)
without doing any multiplication or division.
694 is the key. That’s how you get the green number.
How about 730 and 708? This time 708 has become the low number of the set. Let’s subject 14 from 730 to get 716. Does it work?
708 (14) + 730 (36) = 716 (50)
Let’s double check the answer by multiplying 36 x 14 and 8 x 14, which is the same as 44 x 14. 616. That’s 100 off of 716.
So let’s try subtraction instead:
730 (36) – 708 (14) = 716 (22)
No need to double check our answer. As it turns out 22 is the green number for 716. 50 should have been suspect from the beginning. Always remember to keep in mind the green number when setting up the equations.
Let’s continue with 720 and 708.
720 (26) – 708 (14) = 706 (12)
Works like a charm!
So now we can try 730 and 720 again to see where we made our error previously. Instead of adding 26 and 36, we should have been subtracting 26 from 36 if the star holds true.
730 (36) – 720 (26) = x (10)
Because the green number is 10, would x be 704 or 684? 730 is 26 more than 704 and 720 is 36 more than 684.
Plug in 704. Multiply 26 x 36. 936. Subtract 16 x 26. – 416. 520. That doesn’t sound right.
Plug in 684. Multiply 46 x 36. 1656. Subtract 36 x 26. – 936. 520 again.
It looks like we’re struck out again.
We know that the answer is:
730 (36) – 720 (26) = 756 (10)
756 was the original top point of our 3D star. Maybe we need to put it back in place now. That would make our low point as 632 again. How does this change our star?
By shortening our star to 725 at the top and 663 at the bottom, we were losing an important dimension to our star. This was effectively cutting the height of the star in half. Instead of 124, it became 62. I think that was my error. The top of the star couldn’t be a lower number than other numbers in the star, and likewise the bottom of the star had to be the lowest number. We need to add symmetry back to the star now that we have figured out the green number system.
Is this how God made stars in the heaven? Or is this how God did the math of the Genesis Flood?
Some 3D Combinations:
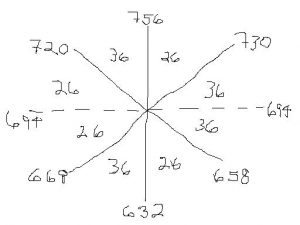
720 + 668 = 52 (694)
730 + 658 = 72 (694)
Straight lines:
756 + 632 = 124 (694)
684 + 704 = 20 (694)
673 + 715 = 42 (694)
720 + 658 = 62 (684)
730 + 668 = 62 (704)
*****
Now that we have created our 3D star in the New Year, let’s see what kind of mathematical applications we can use to make our calculations easier.
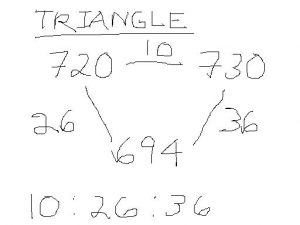
In our 694 star we can see that a triangle is created by the numbers 684, 694, 704, with each side of the triangle being 10. We calculated that:
684 (10) + 704 (10) = 694 (20)
But this knowledge would only apply to a larger number that can be divided by all three numbers. Where are we going to find such a number? I have no idea!
But let’s say we know that 177000 is divisible by 708, which is 250, from past experience. All we need to do is plug 708 into the triangle. The other points now become 698 and 718.
708 x 20 = 14160
177000 / 14160 = 12.5
6980 x 12.5 = 87250
7180 x 12.5 = 89750
177000 / 2 = 88500
88500 – 87250 = 1250
88500 – 89750 = – 1250
We have divided our original number (177000) into two halves of 698 (125) + 718 (125) = 708 (250).
This is how we apply our 3D star to problems. If we want to make an even cut by 2, that is going to create two equals. But if we make the cut using two different numbers in our triangle, the result is not going to be equal because one number is 20 higher than the other.
This may seem confusing at first, but could be useful later on. One value is in having whole numbers instead of fractions to work with in a complex number problem. As long as the numbers that you put at the points of your triangle have some relationship to the number you are dividing, it makes the arithmetic much simpler to do.
*****
We just worked on the horizontal line through the center of our star with the center being 708 and the outer points as 698 and 718.
The vertical line through the center forms another triangle with the points 674, 708, 742. Thus, the same relations as the vertical can be set up:
674 (34) + 742 (34) = 708 (68)
708 (68) = 48144
The other points on our 708 star are 720, 730, 686, and 696 which are 12, 22, -22, -12 in relation to 708.
We can also construct triangles with these numbers, 720 708 730, and 686 708 696. We now have 4 triangles.
All the same relationships that existed in the 694 star exist in the 708 star also:
730 (22) – 720 (12) = 742 (10)
That’s an overview of the 708 3D star!